(생물학, 의학) ¶
(수학, esp 위상수학,topology) ¶
Closure_(topology)= https://en.wikipedia.org/wiki/Closure_(topology)
= https://en.wikipedia.org/wiki/Closure_(topology)
{
(TOC전까지 인용)
"In topology, the closure of a subset $\displaystyle S$ of points in a topological space consists of
Union_(set_theory) of
and also as
the intersectionIntersection_(set_theory) of all closed sets containing $\displaystyle S.$
Intuitively, the closure can be thought of as all the points that are either in $\displaystyle S$ or "very near" S.
A point which is in the closure of $\displaystyle S$ is a point of closureAdherent_point of $\displaystyle S.$ // 
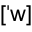adherent_point 
adherent point 
adherent point ...
The notion of closure is in many ways dualDuality_(mathematics)... 쌍대,dual 쌍대성,duality to the notion of interiorInterior_(topology).
}all pointsTopology_glossary#P in $\displaystyle S$ together with
all limit pointsLimit_points ....극한점,limit_point of $\displaystyle S.$
The closure of $\displaystyle S$ may equivalently be defined as the unionTopology_glossary#P in $\displaystyle S$ together withall limit points
Limit_points ....극한점,limit_point of $\displaystyle S.$Union_(set_theory) ofand also as
the intersection
Intersection_(set_theory) of all closed sets containing $\displaystyle S.$Intuitively, the closure can be thought of as all the points that are either in $\displaystyle S$ or "very near" S.
A point which is in the closure of $\displaystyle S$ is a point of closure
Adherent_point of $\displaystyle S.$ // adherent_point adherent point adherent point ...The notion of closure is in many ways dual
Duality_(mathematics)... 쌍대,dual 쌍대성,duality to the notion of interiorInterior_(topology).
폐포_(위상수학) = https://ko.wikipedia.org/wiki/폐포_(위상수학)"주어진 위상공간,topological_space의 부분집합,subset을 포함하는 가장 작은 닫힌집합,closed_set이다. 이건 그 부분집합의 원소와 극한점,limit_point으로 구성된다. ..."
MKLpoint_of_closure ...
point_of_closure =,point_of_closure .
폐포 - 관련표현 15개 정도}