MKL 시리즈,series ? - yes. series is 시리즈 via https://kornorms.korean.go.kr/
=시리즈,series =,series 시리즈 series
{
급수,series가 아닌 다른 series에 대하여.
=시리즈,series =,series 시리즈 series
{
급수,series가 아닌 다른 series에 대하여.
MKL:
serial - 단어간의 정확한 관계 tbw { series serial }
sequential / 시퀀스,sequence - 뜻은 유사할텐데... 차이? (수학에서는 수열,sequence/급수,series의 뜻으로 쓰고 있고, 단어 뜻.)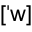 sequence
sequence 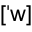 series { series sequence }
series { series sequence }
serial - 단어간의 정확한 관계 tbw { series serial }
sequential / 시퀀스,sequence - 뜻은 유사할텐데... 차이? (수학에서는 수열,sequence/급수,series의 뜻으로 쓰고 있고, 단어 뜻.)
(wikiadmin, tmp) pagename checked: series -> 시리즈 via kornorms.
}
}
1. 거듭제곱 급수, 멱급수, power series ¶
정의:
$\displaystyle x$ 에 대한 멱급수
수렴반지름 $\displaystyle R=1$
$\displaystyle x$ 에 대한 멱급수
$\displaystyle \sum_{n=0}^{\infty}c_nx^n=c_0+c_1x+c_2x^2+\cdots$
$\displaystyle x-a$ 의 거듭제곱급수, $\displaystyle x-a$ 의 멱급수, 중심이 $\displaystyle a$ 인 멱급수$\displaystyle \sum_{n=0}^\infty c_n (x-a)^n=c_0+c_1(x-a)+c_2(x-a)^2+\cdots$
ex.$\displaystyle \sum_{n=0}^\infty \frac{(x-2)^n}{n}$ 은 $\displaystyle x$ 가 어떤 값일 때 수렴하는가?
sol.$\displaystyle \lim_{n\to\infty}\left|\frac{\frac{(x-2)^{n+1}}{n+1}}{\frac{(x-2)^n}{n}}\right|$
$\displaystyle =\lim_{n\to\infty}\frac{n}{n+1}\frac{|x-2|^{n+1}}{|x-2|^n}$
$\displaystyle =\lim_{n\to\infty}\frac{n}{n+1}|x-2|$
$\displaystyle =|x-2|\lim_{n\to\infty}\frac{n}{n+1}$
$\displaystyle =|x-2|$
따라서 비율판정법에 의해$\displaystyle =\lim_{n\to\infty}\frac{n}{n+1}\frac{|x-2|^{n+1}}{|x-2|^n}$
$\displaystyle =\lim_{n\to\infty}\frac{n}{n+1}|x-2|$
$\displaystyle =|x-2|\lim_{n\to\infty}\frac{n}{n+1}$
$\displaystyle =|x-2|$
$\displaystyle |x-2|<1$ 이면 수렴,
$\displaystyle |x-2|>1$ 이면 발산
$\displaystyle |x-2|=1\Rightarrow$
따라서$\displaystyle |x-2|>1$ 이면 발산
$\displaystyle |x-2|=1\Rightarrow$
$\displaystyle x=1$ 일때 : $\displaystyle \sum_{n=1}^{\infty}\frac{(-1)^n}{n}$ 은 수렴 (교대급수판정법에 의해)
$\displaystyle x=3$ 일 때: $\displaystyle \sum_{n=1}^{\infty}\frac1n$ 은 발산
$\displaystyle x=3$ 일 때: $\displaystyle \sum_{n=1}^{\infty}\frac1n$ 은 발산
$\displaystyle 1\le x < 3$ 일때 주어진 급수는 수렴
$\displaystyle x<1\text{ or }x\ge3$ 일때 주어진 급수는 발산
수렴구간은 $\displaystyle [1,3)$$\displaystyle x<1\text{ or }x\ge3$ 일때 주어진 급수는 발산
수렴반지름 $\displaystyle R=1$
1.1. 정리 ¶
거듭제곱급수
sol.
$\displaystyle \Leftrightarrow |x-1|<\sqrt{2}$
$\displaystyle \Leftrightarrow 1-\sqrt{2}
따라서
$\displaystyle |x-1|<\sqrt{2}$ 이면 수렴,
$\displaystyle |x-1|>\sqrt{2}$ 이면 발산.
따라서
수렴반지름 $\displaystyle R=\sqrt{2}$
$\displaystyle \sum_{n=0}^\infty c_n(x-a)^n$
은 반드시 다음 3가지 중 하나만 성립한다.(i) $\displaystyle x=a$ 일 때만 수렴
(ii) 모든 실수 $\displaystyle x$ 에서 수렴
(iii) 적당한 양수 $\displaystyle R$ 이 존재하여
ex.(ii) 모든 실수 $\displaystyle x$ 에서 수렴
(iii) 적당한 양수 $\displaystyle R$ 이 존재하여
$\displaystyle |x-a| 이면 수렴,
$\displaystyle |x-a|>R$ 이면 발산.
이때 $\displaystyle R$ 을 수렴반지름(radius of convergence) 또는 수렴반경이라 부른다.
또한 거듭제곱급수가 수렴하는 구간을 수렴구간이라 부른다.
$\displaystyle |x-a|>R$ 이면 발산.
이때 $\displaystyle R$ 을 수렴반지름(radius of convergence) 또는 수렴반경이라 부른다.
또한 거듭제곱급수가 수렴하는 구간을 수렴구간이라 부른다.
$\displaystyle \sum_{n=0}^\infty \frac{(x-1)^{2n}}{2^n}$
의 수렴반지름과 수렴구간을 구하라.sol.
거듭제곱근 판정법을 쓰면
$\displaystyle \lim_{n\to\infty}\sqrt[n]{\frac{|x-1|^{2n}}{2^n}}$
$\displaystyle =\lim_{n\to\infty}\frac{|x-1|^2}{2}$
$\displaystyle =\frac{|x-1|^2}{2}<1$
$\displaystyle \Leftrightarrow (x-1)^2<2$$\displaystyle \lim_{n\to\infty}\sqrt[n]{\frac{|x-1|^{2n}}{2^n}}$
$\displaystyle =\lim_{n\to\infty}\frac{|x-1|^2}{2}$
$\displaystyle =\frac{|x-1|^2}{2}<1$
$\displaystyle \Leftrightarrow |x-1|<\sqrt{2}$
$\displaystyle \Leftrightarrow 1-\sqrt{2}
따라서
$\displaystyle |x-1|<\sqrt{2}$ 이면 수렴,
$\displaystyle |x-1|>\sqrt{2}$ 이면 발산.
따라서
수렴반지름 $\displaystyle R=\sqrt{2}$
$\displaystyle x=1-\sqrt{2} \Rightarrow \sum\frac{(-\sqrt{2})^{2n}}{2^n}=\sum\frac{2^n}{2^n}=\sum_{n=0}^{\infty}1$ (발산)
$\displaystyle x=1+\sqrt{2} \Rightarrow \sum\frac{\sqrt{2}^{2n}}{2^n}=\sum\frac{2^n}{2^n}=\sum_{n=0}^{\infty}1$ (발산)
따라서 수렴구간은 $\displaystyle (1-\sqrt{2},1+\sqrt{2})$
$\displaystyle x=1+\sqrt{2} \Rightarrow \sum\frac{\sqrt{2}^{2n}}{2^n}=\sum\frac{2^n}{2^n}=\sum_{n=0}^{\infty}1$ (발산)
따라서 수렴구간은 $\displaystyle (1-\sqrt{2},1+\sqrt{2})$
1.2. 거듭제곱급수에 의한 함수 표현 ¶
고딩때 알고있는것
$\displaystyle a+ar+ar^2+\cdots=\frac{a}{1-r}\quad(|r|<1)$
ex.$\displaystyle \frac1{1-x}=1+x+x^2+x^3+\cdots=\sum_{n=0}^{\infty}x^n$
단 $\displaystyle (|x|<1)$
$\displaystyle \frac1{1+x^2}=\frac1{1-(-x^2)}=1-x^2+x^4-x^6+\cdots$
ex.단 $\displaystyle (|x|<1)$
$\displaystyle \frac1{1+x^2}=\frac1{1-(-x^2)}=1-x^2+x^4-x^6+\cdots$
$\displaystyle =\sum_{n=0}^{\infty}(-1)^nx^{2n}$
단 $\displaystyle (|x|<1)$왜냐하면 $\displaystyle |-x^2|<1$
$\displaystyle \Leftrightarrow |x^2|<1$
$\displaystyle \Leftrightarrow |x|^2<1$
$\displaystyle \Leftrightarrow |x|<1$
$\displaystyle \Leftrightarrow |x^2|<1$
$\displaystyle \Leftrightarrow |x|^2<1$
$\displaystyle \Leftrightarrow |x|<1$
$\displaystyle \frac{x^2}{x+3}=x^2\left(\frac1{3+x}\right)=\frac{x^2}{3}\left(\frac1{1+\frac{x}3}\right)=\frac{x^2}{3}\left(\frac1{1-\left(-\frac{x}3\right)}\right)$
$\displaystyle =\frac{x^2}{3}\left(1-\frac{x}3+\frac{x^2}9-\frac{x^3}{27}+\cdots\right)$
$\displaystyle =\frac{x^2}{3}\sum_{n=0}^{\infty}(-1)^n \frac{x^n}{3^n}$
$\displaystyle =\sum_{n=0}^{\infty}(-1)^n \frac{x^{n+2}}{3^{n+1}} \;\; (-3
$\displaystyle =\frac{x^2}{3}\left(1-\frac{x}3+\frac{x^2}9-\frac{x^3}{27}+\cdots\right)$
$\displaystyle =\frac{x^2}{3}\sum_{n=0}^{\infty}(-1)^n \frac{x^n}{3^n}$
$\displaystyle =\sum_{n=0}^{\infty}(-1)^n \frac{x^{n+2}}{3^{n+1}} \;\; (-3
조건은 왜냐하면
$\displaystyle \left|-\frac{x}3\right|<1$
$\displaystyle \Leftrightarrow |x|<3$
$\displaystyle \Leftrightarrow -3
$\displaystyle \left|-\frac{x}3\right|<1$
$\displaystyle \Leftrightarrow |x|<3$
$\displaystyle \Leftrightarrow -3
1.3. 멱급수의 미적분 ¶
정리:
$\displaystyle f(x)=\sum_{n=0}^\infty c_n(x-a)^n$ 의 수렴반지름이 $\displaystyle R$ 이면
$\displaystyle f$ 는 $\displaystyle (a-R,a+R)$ 에서 미분 및 적분 가능하고,
$\displaystyle \text{(i) }f'(x)=\sum_{n=1}^\infty n c_n (x-a)^{n-1}$
$\displaystyle \text{(ii) }\int f(x) dx= c + \sum_{n=0}^{\infty} \frac{c_n}{n+1}(x-a)^{n+1}$
이며 (i),(ii)의 수렴반지름은 역시 $\displaystyle R$ 이다.
$\displaystyle f$ 는 $\displaystyle (a-R,a+R)$ 에서 미분 및 적분 가능하고,
$\displaystyle \text{(i) }f'(x)=\sum_{n=1}^\infty n c_n (x-a)^{n-1}$
$\displaystyle \text{(ii) }\int f(x) dx= c + \sum_{n=0}^{\infty} \frac{c_n}{n+1}(x-a)^{n+1}$
이며 (i),(ii)의 수렴반지름은 역시 $\displaystyle R$ 이다.
1.4. ex. 1/(1-x)² ¶
ex.
$\displaystyle \frac1{(1-x)^2}$ 을 멱급수로 나타내라.
sol.$\displaystyle \frac1{1-x}=1+x+x^2+\cdots=\sum_{n=0}^{\infty}x^n\;(R=1)$
미분하면$\displaystyle \frac1{(1-x)^2}=1+2x+3x^2+\cdots$
$\displaystyle =\sum_{n=0}^{\infty}nx^{n-1}$
$\displaystyle =\sum_{n=1}^{\infty}nx^{n-1}$ (이게 더 옳다고..)
$\displaystyle =\sum_{n=0}^{\infty}(n+1)x^n$ (n제곱으로 표현, 이게 더 좋은 표현이라고..)
$\displaystyle =\sum_{n=1}^{\infty}nx^{n-1}$ (이게 더 옳다고..)
$\displaystyle =\sum_{n=0}^{\infty}(n+1)x^n$ (n제곱으로 표현, 이게 더 좋은 표현이라고..)
1.5. ex. ln(1+x) ¶
ex.
즉, $\displaystyle \ln(1+x)=x-\frac{x^2}2+\frac{x^3}3-\frac{x^4}4+\cdots\;\;(-1
$\displaystyle \ln(1+x)$ 의 멱급수표현을 구하라
sol.$\displaystyle \ln(1+x)=\int\frac1{1+x}dx\;(x>-1)$
$\displaystyle =\int(1-x+x^2-x^3+\cdots)dx\;(-1
$\displaystyle =c+x-\frac12x^2+\frac13x^3-\frac14x^4+\cdots\;(-1
$\displaystyle =\sum_{n=1}^{\infty}(-1)^{n-1} \frac{x^n}{n}+c \;(-1
c를 결정하려면 수렴구간중 적당한 값을 대입해본다. 0을 대입하면$\displaystyle =\int(1-x+x^2-x^3+\cdots)dx\;(-1
$\displaystyle =c+x-\frac12x^2+\frac13x^3-\frac14x^4+\cdots\;(-1
$\displaystyle =\sum_{n=1}^{\infty}(-1)^{n-1} \frac{x^n}{n}+c \;(-1
$\displaystyle x=0\Rightarrow 0=\ln1=c$
따라서$\displaystyle \ln(1+x)=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}x^n\;(-1
실제로 위의 식은 $\displaystyle x=1$ 일 때도 성립한다는 것이 알려져 있다. (아벨의 극한정리)즉, $\displaystyle \ln(1+x)=x-\frac{x^2}2+\frac{x^3}3-\frac{x^4}4+\cdots\;\;(-1
ex. $\displaystyle x=1:$
$\displaystyle 1-\frac12+\frac13-\frac14+\cdots=\ln 2$ (조화급수)
ex. $\displaystyle x=-\frac12:$$\displaystyle -\ln2=\ln\frac12=-\frac12-\frac12\cdot\frac1{2^2}-\frac13\cdot\frac1{2^3}-\frac14\cdot\frac1{2^4}{}-{}\cdots$
$\displaystyle \ln2=\frac12+\frac12\cdot\frac1{2^2}+\frac13\cdot\frac1{2^3}+\cdots$
$\displaystyle \ln2=\frac12+\frac12\cdot\frac1{2^2}+\frac13\cdot\frac1{2^3}+\cdots$
$\displaystyle =\sum_{n=1}^{\infty}\frac1{n2^n}$
1.6. ex. arctan(x) ¶
ex. $\displaystyle f(x)=\tan^{-1}x$ 의 멱급수 표현을 구하라.
sol.
therefore,
$\displaystyle \tan^{-1}x=\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}x^{2n+1}\;\;(-1
실제로는 $\displaystyle -1\le x\le 1$ 일 때 위의 식이 성립한다.
therefore,
$\displaystyle \tan^{-1}x=x-\frac{x^3}3+\frac{x^5}5-\frac{x^7}7+\cdots\;\;(-1\le x\le1)$
sol.
$\displaystyle f'(x)=\frac1{1+x^2}$ 이므로
$\displaystyle \tan^{-1}x=f(x)=\int \frac{1}{1+x^{2}} dx$
$\displaystyle =\int\left[\sum_{n=0}^\infty(-x^2)^n\right]dx\;(|x|<1)$
$\displaystyle =\sum_{n=0}^\infty\int(-1)^n x^{2n} dx \;(|x|<1)$
$\displaystyle =\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}x^{2n+1}+C$
$\displaystyle x=0\Rightarrow 0=\tan^{-1}0=0+C$$\displaystyle \tan^{-1}x=f(x)=\int \frac{1}{1+x^{2}} dx$
$\displaystyle =\int\left[\sum_{n=0}^\infty(-x^2)^n\right]dx\;(|x|<1)$
$\displaystyle =\sum_{n=0}^\infty\int(-1)^n x^{2n} dx \;(|x|<1)$
$\displaystyle =\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}x^{2n+1}+C$
therefore,
$\displaystyle \tan^{-1}x=\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}x^{2n+1}\;\;(-1
실제로는 $\displaystyle -1\le x\le 1$ 일 때 위의 식이 성립한다.
therefore,
$\displaystyle \tan^{-1}x=x-\frac{x^3}3+\frac{x^5}5-\frac{x^7}7+\cdots\;\;(-1\le x\le1)$
ex. $\displaystyle x=1\Rightarrow\frac{\pi}4=\tan^{-1}1=1-\frac13+\frac15-\frac17+\cdots$
 멱급수,power_series
멱급수,power_series
therefore, $\displaystyle \pi=4\left(1-\frac13+\frac15-\frac17+\cdots\right)$
see also 2. 테일러급수와 매클로린급수 ¶
만일 $\displaystyle f$ 가 거듭제곱급수로 표현된다면, 즉
$\displaystyle f(x)=c_0+c_1(x-1)+c_2(x-a)^2+c_3(x-a)^3+c_4(x-a)^4+\cdots\;\;(|x-a|
이라면 $\displaystyle x=a$ 대입하여$\displaystyle f(a)=c_0$
미분하여$\displaystyle f'(x)=c_1+2c_2(x-a)+3c_3(x-a)^2+4c_4(x-a)^3+\cdots$
$\displaystyle f'(a)=c_1$
또 미분하여$\displaystyle f'(a)=c_1$
$\displaystyle f''(x)=2c_2+3\cdot 2c_3(x-a)+4\cdot 3c_4(x-a)^2+\cdots$
$\displaystyle f''(a)=2c_2$
또 미분하여$\displaystyle f''(a)=2c_2$
$\displaystyle f'''(x)=3\cdot 2 c_3+4\cdot 3\cdot 2 c_4 (x-a)+\cdots$
$\displaystyle f'''(a)=3\cdot 2 c_3$
therefore$\displaystyle f'''(a)=3\cdot 2 c_3$
$\displaystyle c_n=\frac{f^{(n)}(a)}{n!}$
정리:$\displaystyle f(x)=\sum_{n=0}^{\infty}c_n(x-a)^n,\;\;\;|x-a|
이라 하면$\displaystyle c_n=\frac{f^{(n)}(a)}{n!}$
이다.참고:
함수 $\displaystyle f$ 가 무한번 미분가능하고,
$\displaystyle a$ 에 관한 거듭제곱급수로 표현된다면,
그 계수는 유일하게 결정된다.
정의:$\displaystyle a$ 에 관한 거듭제곱급수로 표현된다면,
그 계수는 유일하게 결정된다.
$\displaystyle f$ 의 거듭제곱 급수 표현이 존재할 경우
특히 $\displaystyle a=0$ 일 때
ex.$\displaystyle f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n$를 $\displaystyle a$ 에서의 $\displaystyle f$ 의 테일러 급수(Taylor series)라 한다.
$\displaystyle =f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\cdots$
특히 $\displaystyle a=0$ 일 때
$\displaystyle f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$를 $\displaystyle f$ 의 매클로린 급수(Maclaurin series)라 한다.
$\displaystyle =f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\cdots$
$\displaystyle f(x)=e^x$ 의 Maclaurin series와 수렴반지름을 구하라.
sol.$\displaystyle f'(x)=e^x,\;f''(x)=e^x,\;\cdots$
$\displaystyle f(0)=f'(0)=f''(0)=\cdots=1$
$\displaystyle \sum_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\cdots$
이고 비율판정법을 쓰면 수렴반지름 R은 ∞이다.$\displaystyle f(0)=f'(0)=f''(0)=\cdots=1$
$\displaystyle \sum_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\cdots$
참고:
따라서 $\displaystyle f$ 의 매클로린 급수는 영함수(0함수)이며 이는 $\displaystyle f$ 와 다르다.
$\displaystyle f(x)=\begin{cases}e^{-\frac1{x^2}}&(x\ne0)\\0&(x=0)\end{cases}$
$\displaystyle \Rightarrow f^{(n)}(0)=0\;\;(n=0,1,2,\cdots)$따라서 $\displaystyle f$ 의 매클로린 급수는 영함수(0함수)이며 이는 $\displaystyle f$ 와 다르다.
정의: 함수 $\displaystyle f$ 에 대해
$\displaystyle R_n(x)=f(x)-T_n(x)$ 를 테일러급수의 나머지항(remainder)이라 부른다.
$\displaystyle T_n(x)=\sum_{k=0}^{n}\frac{f^{(k)}(a)}{k!}(x-a)^k$를 $\displaystyle a$ 에서 $\displaystyle f$ 의 $\displaystyle n$ 차 테일러다항식이라 부른다.
$\displaystyle R_n(x)=f(x)-T_n(x)$ 를 테일러급수의 나머지항(remainder)이라 부른다.
정리:
$\displaystyle |x-a| 일 때
$\displaystyle f(x)=T_n(x)+R_n(x)$ 이고
$\displaystyle \lim_{n\to\infty}R_n(x)=0$ 이면
$\displaystyle f(x)=\lim_{n\to\infty}T_n(x)=\sum_{k=0}^{\infty}\frac{f^{(k)}(a)}{k!}(x-a)^k$ 이다.
정리(테일러의 공식)$\displaystyle f(x)=T_n(x)+R_n(x)$ 이고
$\displaystyle \lim_{n\to\infty}R_n(x)=0$ 이면
$\displaystyle f(x)=\lim_{n\to\infty}T_n(x)=\sum_{k=0}^{\infty}\frac{f^{(k)}(a)}{k!}(x-a)^k$ 이다.
$\displaystyle f$ 의 $\displaystyle (n+1)$ 계 도함수가 $\displaystyle a$ 를 포함하는 적당한 구간 $\displaystyle I$ 에서 존재할 때, $\displaystyle I$ 에 속한 $\displaystyle x$ 에 대하여 $\displaystyle x$ 와 $\displaystyle a$ 사이에 적당한 실수 $\displaystyle z$ 가 존재하여
$\displaystyle R_n(x)=\frac{f^{(n+1)}(z)}{(n+1)!}(x-a)^{n+1}$
이다.$\displaystyle R_n(x)=\frac{f^{(n+1)}(z)}{(n+1)!}(x-a)^{n+1}$
참고:
(i) 위의 식을 다시 쓰면
$\displaystyle f(x)=\underbrace{f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n}_{T_n(x)}+\underbrace{\frac{f^{(n+1)}(z)}{(n+1)!}(x-a)^{n+1}}_{R_n(x)}$
(ii)
$\displaystyle n=0$ 이면,
$\displaystyle f(x)=f(a)+f'(z)(x-a)$ 즉
$\displaystyle f(x)-f(a)=f'(z)(x-a)$ (평균값 정리를 일반화한 거라고 볼 수 있다)
(i) 위의 식을 다시 쓰면
$\displaystyle f(x)=\underbrace{f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n}_{T_n(x)}+\underbrace{\frac{f^{(n+1)}(z)}{(n+1)!}(x-a)^{n+1}}_{R_n(x)}$
(ii)
$\displaystyle n=0$ 이면,
$\displaystyle f(x)=f(a)+f'(z)(x-a)$ 즉
$\displaystyle f(x)-f(a)=f'(z)(x-a)$ (평균값 정리를 일반화한 거라고 볼 수 있다)
정리: $\displaystyle \forall x\in\mathbb{R},$
∴ $\displaystyle \lim_{n\to\infty}R_n(x)=0$
따라서
$\displaystyle f(x)=e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}(x\in\mathbb{R})$
$\displaystyle \lim_{n\to\infty}\frac{x^n}{n!}=0$
pf.$\displaystyle \sum_{n=0}^{\infty}\frac{x^n}{n!}$ 은 임의의 $\displaystyle x$ 에 대해 수렴한다. (<= 비율판정법)
따라서 0이다.
예:따라서 0이다.
$\displaystyle e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\;\;(x\in\mathbb{R})$
pf.$\displaystyle x=0$ 일 때 : 자명하게 위의 식이 성립.
$\displaystyle x\ne0$ 일 때 : 테일러 공식에서 주어진 $\displaystyle x(\ne0)$ 에 대하여
$\displaystyle -|x|\lt z\lt |x|$ 인 $\displaystyle z$ 가 존재하여
$\displaystyle R_n(x)=\frac{e^z}{(n+1)!}x^{n+1}$ 이다.
∴$\displaystyle x\ne0$ 일 때 : 테일러 공식에서 주어진 $\displaystyle x(\ne0)$ 에 대하여
$\displaystyle -|x|\lt z\lt |x|$ 인 $\displaystyle z$ 가 존재하여
$\displaystyle R_n(x)=\frac{e^z}{(n+1)!}x^{n+1}$ 이다.
$\displaystyle |R_n(x)|\le \frac{e^{ | x | }}{(n+1)!}|x|^{n+1}\to0$ ( $\displaystyle n\to\infty$ 일때 )
∴ $\displaystyle \lim_{n\to\infty}|R_n(x)|=0$∴ $\displaystyle \lim_{n\to\infty}R_n(x)=0$
따라서
$\displaystyle f(x)=e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}(x\in\mathbb{R})$
$\displaystyle e=\sum_{n=0}^{\infty}\frac1{n!}=1+\frac1{1!}+\frac1{2!}+\frac1{3!}+\cdots$
$\displaystyle \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots\;(x\in\mathbb{R})$
$\displaystyle \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\;(x\in\mathbb{R})$
$\displaystyle \tan^{-1}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots\;(-1\le x\le1)$
$\displaystyle \ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots\;(-1
(이것들은 암기)
3. 이항급수 ¶
$\displaystyle (1+x)^2=1+2x+x^2\\(1+x)^3=1+3x+3x^2+x^3$
$\displaystyle k$ 가 자연수일 때
$\displaystyle \binom{k}{n}=\frac{k(k-1)\cdots(k-n+1)}{n!}$
$\displaystyle f(x)=(1+x)^k,\;f(0)=1$
$\displaystyle f'(x)=k(1+x)^{k-1},\;f'(0)=k$
$\displaystyle f{ } ' '(x)=k(k-1)(1+x)^{k-2},\;f{ } ' '(0)=k(k-1)$
$\displaystyle f^{(n)}(0)=k(k-1)(k-2)\cdots(k-n+1)$
$\displaystyle (1+x)^k=\sum_{n=0}^k\binom{k}{n}x^n$$\displaystyle \binom{k}{0}=1,$
$\displaystyle \binom{k}{n}=\frac{k(k-1)\cdots(k-n+1)}{n!}$
$\displaystyle (n=1,2,3,\cdots,k)$
$\displaystyle k$ 가 실수일 때$\displaystyle f(x)=(1+x)^k,\;f(0)=1$
$\displaystyle f'(x)=k(1+x)^{k-1},\;f'(0)=k$
$\displaystyle f{ } ' '(x)=k(k-1)(1+x)^{k-2},\;f{ } ' '(0)=k(k-1)$
$\displaystyle \vdots$
$\displaystyle f^{(n)}(x)=k(k-1)(k-2)\cdots(k-n+1)(1+x)^{k-n},$$\displaystyle f^{(n)}(0)=k(k-1)(k-2)\cdots(k-n+1)$
따라서 $\displaystyle f(x)=(1+x)^k$ 의 매클로린 급수는
$\displaystyle \sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n=1+\sum_{n=1}^{\infty}\frac{k(k-1)(k-2)\cdots(k-n+1)}{n!}x^n$
참고
(i) 비율판정법을 사용하면 수렴반지름 $\displaystyle R=1$
따라서
$\displaystyle k$ 가 임의의 실수이고 $\displaystyle |x|<1$ 이면
$\displaystyle \binom{k}{0}=1,\;\binom{k}{n}=\frac{k(k-1)\cdots(k-n+1)}{n!}\;\;\;\;(n=1,2,3,\cdots)$
(i) 비율판정법을 사용하면 수렴반지름 $\displaystyle R=1$
따라서
$\displaystyle |x|<1\Rightarrow$ 수렴
$\displaystyle |x|>1\Rightarrow$ 발산
$\displaystyle |x|=1\Rightarrow$ $\displaystyle k$ 값에 따라 수렴여부가 달라짐
(ii)$\displaystyle |x|>1\Rightarrow$ 발산
$\displaystyle |x|=1\Rightarrow$ $\displaystyle k$ 값에 따라 수렴여부가 달라짐
$\displaystyle \lim_{n\to\infty}R_n(x)=0$
정리(이항급수)$\displaystyle k$ 가 임의의 실수이고 $\displaystyle |x|<1$ 이면
$\displaystyle (1+x)^k=1+kx+\frac{k(k-1)}{2!}x^2+\frac{k(k-1)(k-2)}{3!}x^3+\cdots$여기서
$\displaystyle =\sum_{n=0}^{\infty}\binom{k}{n}x^n$
$\displaystyle \binom{k}{0}=1,\;\binom{k}{n}=\frac{k(k-1)\cdots(k-n+1)}{n!}\;\;\;\;(n=1,2,3,\cdots)$
참고:
(i) k가 자연수이면 n>k일 때
따라서 수렴반지름 R=2이다.
(i) k가 자연수이면 n>k일 때
$\displaystyle \binom{k}{n}=0$ 이다.
ex.$\displaystyle \binom{2}{3}=\frac{2\cdot1\cdot0}{3!}=0$
$\displaystyle \binom{2}{4}=\frac{2\cdot1\cdot0\cdot(-1)}{4!}=0$
(ii) 예:$\displaystyle \binom{2}{4}=\frac{2\cdot1\cdot0\cdot(-1)}{4!}=0$
$\displaystyle \binom{3}{2}=\frac{3\cdot2}{2!}=3(={}_3\textrm{C}_2)$
$\displaystyle \binom{\frac{3}{2}}{3}=\frac{\frac32\cdot\frac12\cdot\left(-\frac12\right)}{3!}=-\frac1{16}$
$\displaystyle \binom{-1}{3}=\frac{(-1)(-2)(-3)}{3!}=-1$
ex.$\displaystyle \binom{\frac{3}{2}}{3}=\frac{\frac32\cdot\frac12\cdot\left(-\frac12\right)}{3!}=-\frac1{16}$
$\displaystyle \binom{-1}{3}=\frac{(-1)(-2)(-3)}{3!}=-1$
$\displaystyle f(x)=\sqrt{2+x}$ 의 매클로린급수와 수렴반지름을 구하라.
sol.$\displaystyle \sqrt{2+x}=\sqrt{2}\sqrt{1+\frac{x}2}=\sqrt{2}\left(1+\frac{x}2\right)^{\frac12}$
$\displaystyle \binom{1/2}{0}=1,$
$\displaystyle \binom{1/2}{1}=1/2,$
$\displaystyle \binom{1/2}{n}=\frac{(\frac12)(-\frac12)(-\frac32)\cdots(\frac12-n+1)}{n!}$
오른쪽 위에 식은 $\displaystyle \left(\frac12-n+1=\frac32-n=\frac{3-2n}{2}=-\frac{2n-3}{2}\right)$$\displaystyle \binom{1/2}{0}=1,$
$\displaystyle \binom{1/2}{1}=1/2,$
$\displaystyle \binom{1/2}{n}=\frac{(\frac12)(-\frac12)(-\frac32)\cdots(\frac12-n+1)}{n!}$
$\displaystyle =(-1)^{n-1}\frac{(\frac12)(\frac12)(\frac32)(\frac52)\cdots(\frac{2n-3}{2})}{n!}$
$\displaystyle =(-1)^{n-1}\frac{1\cdot3\cdot 5\cdots (2n-3)}{n!2^n}\;\;(n\ge2)$
∴ 매클로린급수는$\displaystyle =(-1)^{n-1}\frac{1\cdot3\cdot 5\cdots (2n-3)}{n!2^n}\;\;(n\ge2)$
$\displaystyle \sqrt{2}\sum_{n=0}^{\infty}\binom{\frac12}{n}\left(\frac{x}{2}\right)^n$
$\displaystyle =\sqrt{2}\left[\binom{1/2}{0}+\binom{1/2}{1}\frac{x}2+\sum_{n=2}^{\infty}\binom{1/2}{n}\left(\frac{x}{2}\right)^n\right]$
$\displaystyle =\sqrt{2}\left[1+\frac{x}{4}+\sum_{n=2}^{\infty}(-1)^{n-1}\frac{1\cdot3\cdot5\cdots(2n-3)}{n!2^n}\cdot\frac{x^n}{2^n}\right]$
$\displaystyle =\sqrt{2}\left[1+\frac{x}{4}+\sum_{n=2}^{\infty}(-1)^{n-1}\frac{1\cdot3\cdot5\cdots(2n-3)}{n!2^{2n}}x^n\right]$
이며, 이 급수는 $\displaystyle |\frac{x}2|<1$ 즉 $\displaystyle |x|<2$ 일 때 수렴.$\displaystyle =\sqrt{2}\left[\binom{1/2}{0}+\binom{1/2}{1}\frac{x}2+\sum_{n=2}^{\infty}\binom{1/2}{n}\left(\frac{x}{2}\right)^n\right]$
$\displaystyle =\sqrt{2}\left[1+\frac{x}{4}+\sum_{n=2}^{\infty}(-1)^{n-1}\frac{1\cdot3\cdot5\cdots(2n-3)}{n!2^n}\cdot\frac{x^n}{2^n}\right]$
$\displaystyle =\sqrt{2}\left[1+\frac{x}{4}+\sum_{n=2}^{\infty}(-1)^{n-1}\frac{1\cdot3\cdot5\cdots(2n-3)}{n!2^{2n}}x^n\right]$
따라서 수렴반지름 R=2이다.
참고: 점점점 $\displaystyle (\cdots)$ 표현을 피하는 법??
$\displaystyle 1\cdot3\cdot5\cdots(2n-3)$
$\displaystyle =\frac{1\cdot2\cdot3\cdot4\cdot5\cdot6\cdots(2n-3)(2n-2)}{2\cdot4\cdot6\cdots(2n-2)}$
$\displaystyle =\frac{(2n-2)!}{2^{n-1}\cdot1\cdot2\cdot3\cdots(n-1)}$
$\displaystyle =\frac{(2n-2)!}{2^{n-1}(n-1)!}$
그리하여 위 문제의 매클로린급수를 다시 표현하면$\displaystyle =\frac{1\cdot2\cdot3\cdot4\cdot5\cdot6\cdots(2n-3)(2n-2)}{2\cdot4\cdot6\cdots(2n-2)}$
$\displaystyle =\frac{(2n-2)!}{2^{n-1}\cdot1\cdot2\cdot3\cdots(n-1)}$
$\displaystyle =\frac{(2n-2)!}{2^{n-1}(n-1)!}$
$\displaystyle \sqrt{2}\left(1+\frac{x}4+\sum_{n=2}^{\infty}(-1)^{n-1}\frac{(2n-2)!}{n!2^{3n-1}(n-1)!}x^n\right)$
$\displaystyle =\sqrt{2}\left(1+\sum_{n=1}^{\infty}(-1)^{n-1}\frac{(2n-2)!}{(n-1)!n!2^{3n-1}}x^n\right)$
$\displaystyle =\sqrt{2}\left(1+\sum_{n=1}^{\infty}(-1)^{n-1}\frac{(2n-2)!}{(n-1)!n!2^{3n-1}}x^n\right)$
3.1. 극한계산에의 응용 ¶
예:
$\displaystyle e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\;(x\in\mathbb{R})$
$\displaystyle e^{ix}=1+ix+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}+\cdots$
$\displaystyle =1+ix-\frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+i\frac{x^5}{5!}+\cdots$
실수부와 허수부를 따로 묶으면
$\displaystyle =\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots\right)+i\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right)$
$\displaystyle =\cos x+i\sin x$
$\displaystyle \lim_{x\to 0}\frac{\tan^{-1}2x-2x}{x^3}$
$\displaystyle =\lim_{x\to 0}\frac{\left(2x-\frac{(2x)^3}{3}+\frac{(2x)^5}{5}-\frac{(2x)^7}{7}+\cdots\right)-2x}{x^3}$
$\displaystyle =\lim_{x\to 0}\left(-\frac83+\frac{32}5x^2-\frac{128}7x^4+\cdots\right)$
$\displaystyle =-\frac83$
ex.$\displaystyle =\lim_{x\to 0}\frac{\left(2x-\frac{(2x)^3}{3}+\frac{(2x)^5}{5}-\frac{(2x)^7}{7}+\cdots\right)-2x}{x^3}$
$\displaystyle =\lim_{x\to 0}\left(-\frac83+\frac{32}5x^2-\frac{128}7x^4+\cdots\right)$
$\displaystyle =-\frac83$
$\displaystyle e^x\cos x$ 의 매클로린급수를 삼차항까지 구하라.
sol.$\displaystyle e^x\cos x=\left(1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\right)\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\right)$
$\displaystyle =1+x+\left(-\frac12+\frac12\right)x^2+\left(-\frac12+\frac16\right)x^3+\cdots$
$\displaystyle =1+x-\frac13x^3+\cdots$
참고: 복소수지수$\displaystyle =1+x+\left(-\frac12+\frac12\right)x^2+\left(-\frac12+\frac16\right)x^3+\cdots$
$\displaystyle =1+x-\frac13x^3+\cdots$
$\displaystyle e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\;(x\in\mathbb{R})$
$\displaystyle e^{ix}=1+ix+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}+\cdots$
$\displaystyle =1+ix-\frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+i\frac{x^5}{5!}+\cdots$
실수부와 허수부를 따로 묶으면
$\displaystyle =\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots\right)+i\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right)$
$\displaystyle =\cos x+i\sin x$
$\displaystyle e^{ix}=\cos x+i\sin x\;\;(x\in\mathbb{R})$로 정의한다.
ex. $\displaystyle e^{2+3i}=e^2e^{3i}=e^2(\cos 3+i\sin 3)$
ex. $\displaystyle e^{\pi i}=\cos\pi+i\sin\pi=-1$
ex. $\displaystyle e^{\pi i}=\cos\pi+i\sin\pi=-1$
